Don Bosco College (Co-Ed), Yelagiri Hills

Design and Analysis of Algorithms (DAA) is a fundamental field in computer science that involves creating efficient solutions to computational problems and evaluating their performance. Here are the key points:

1. Algorithm Design:

   • Involves creating step-by-step instructions (algorithms) to solve specific problems.
   • Focuses on designing efficient, correct, and practical algorithms.
   • Aims to find optimal solutions by considering factors like time complexity, space complexity, and correctness.

2. Algorithm Analysis:

   • Evaluates the efficiency of algorithms.
   • Key aspects:
     • Time Complexity: Measures how the running time of an algorithm grows with input size.
     • Space Complexity: Measures the memory used by an algorithm.
     • Asymptotic Notations: Expresses complexity in terms of upper and lower bounds (e.g., Big O, Omega, Theta).
     • Worst, Average, and Best Case Analysis: Considers different scenarios.
     • Loop Analysis: Examines loops within algorithms.
     • Recurrence Relations: Analyzes recursive algorithms.
     • Amortized Analysis: Deals with average cost over a sequence of operations

     • Topics Covered:

       • Divide and conquer
       • Randomization
       • Dynamic programming
       • Greedy algorithms

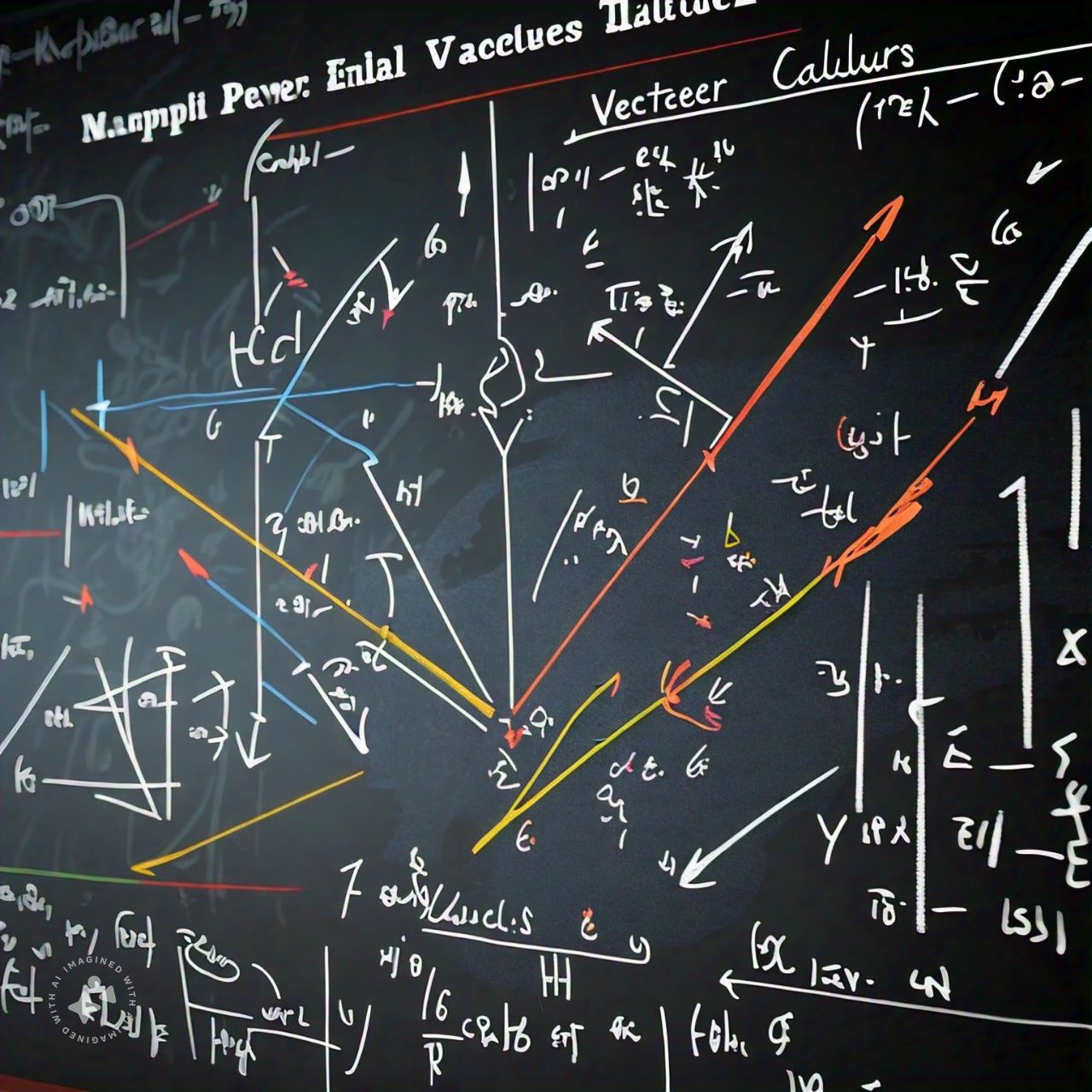
1.Vector Fields

• A vector field assigns a vector to every point in a region of space.
• Example: The gravitational field, where each point has a vector pointing towards the Earth’s center.

2. Gradient (∇f)

• The gradient of a scalar field $f(x, y, z)$ is a vector field that points in the direction of the greatest rate of increase of the function.
• Mathematically: $\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)$.
• Application: Used in physics to find the direction of the steepest ascent.

3. Divergence (∇ · F)

• The divergence of a vector field $\mathbf{F}$ measures the rate at which "stuff" is expanding from a point.
• Mathematically: $\nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}$.
• Application: Used to describe sources or sinks in fluid flow.

4. Curl (∇ × F)

• The curl of a vector field $\mathbf{F}$ measures the rotation or the swirling strength of the field around a point.
• Mathematically: $\nabla \times \mathbf{F} = \left( \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}, \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}, \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \right)$.
• Application: Important in electromagnetism (e.g., Faraday’s Law of Induction).

5. Line Integrals

• The line integral of a vector field along a curve measures the work done by the field in moving a particle along that curve.
• Mathematically: $\int_C \mathbf{F} \cdot d\mathbf{r}$, where $d\mathbf{r}$ is a differential element of the curve $C$.

6. Surface Integrals

• The surface integral extends the concept of line integrals to surfaces. It measures the flow of a vector field across a surface.
• Mathematically: $\int_S \mathbf{F} \cdot d\mathbf{S}$, where $d\mathbf{S}$ is a differential element of the surface $S$.

7. Theorems

• Gradient Theorem: Relates a line integral of a gradient field to the difference in the scalar field at the endpoints.
• Divergence Theorem (Gauss's Theorem): Converts a surface integral over a closed surface to a volume integral of the divergence over the region inside.
• Stokes' Theorem: Relates a surface integral of the curl of a vector field over a surface to a line integral of the vector field around the boundary curve of the surface.